Ämnet för den här artikeln är beräkningen av en polykarbonatkapell med dina egna händer. Vi måste lära oss hur man beräknar huvudparametrarna för strukturen i samband med dess styrka och dimensioner. Låt oss gå.

Vad beräknar vi
Vi måste lära oss hur man räknar:
- Tjockleken på polykarbonatet och backens stigning beroende på förväntad snölast per kvadratmeter.
- Mått på valvetäckning (vilket i termer av geometri handlar om att beräkna längden på bågen).
För att förtydliga: vi undersöker sätt att beräkna bågen för känd radie och vinkel för sektorn, såväl som för fallet då vi bara känner till avstånden mellan bågytans extrempunkter.
- Minsta rörsektion med en känd böjbelastning.
I den här ordningen går vi vidare.
Svarv och beläggningstjocklek
Låt oss börja med beräkningen av snölasten.
Innan vi tar reda på hur man beräknar en polykarbonatkapell kommer vi att formulera ett par antaganden som beräkningen bygger på.
- De givna uppgifterna är relevanta för material av hög kvalitet utan tecken på förstörelse av ultraviolett strålning. Polykarbonat utan UV-filter blir skört efter 2-3 års drift i ljuset.

- Vi försummar medvetet den begränsade deformationsstabiliteten hos lådan, eftersom den anser att den är absolut stark.
Och nu - ett bord som hjälper dig att välja den optimala tjockleken på polykarbonat och stigningen på lådan.
| Belastning, kg/m2 | Lådcellsmått med polykarbonattjocklek, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200x900 | 1320 x 920 | 1250x950 |
| 900 x 900 | 950 x 950 | 1000x1000 | 1100x1100 | |
| 820 x 1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880 x 660 | 1000x750 | 1050x750 | 1150x900 |
| 760 x 760 | 830 x 830 | 830 x 830 | 970 x 970 | |
| 700 x 860 | 750 x 900 | 750 x 950 | 850 x 1050 | |
| 200 | 800x600 | 850 x 650 | 950x700 | 1100x850 |
| 690 x 690 | 760 x 760 | 780 x 780 | 880 x 880 | |
| 620 x 780 | 650 x 850 | 700 x 850 | 750 x 950 | |
Båge
Beräkning efter radie och sektor
Hur beräknar man bågen för en baldakin om vi känner till böjradien och bågsektorn?

Formeln kommer att se ut som P=pi*r*n/180, där:
- P är längden på bågen (i vårt fall, längden på ett polykarbonatark eller ett profilrör, som kommer att bli ett element i ramen).
- pi är talet "pi" (i beräkningar som inte kräver extremt hög noggrannhet, vanligtvis lika med 3,14).
- r är bågens radie.
- n är bågvinkeln i grader.
Låt oss, som ett exempel, med våra egna händer beräkna längden på baldakinbågen med en radie på 2 meter och en sektor på 35 grader.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 meter.
Under arbetets gång uppstår ofta den motsatta situationen: det är nödvändigt att justera bågens radie och sektor till en fast längd på bågen. Skälen är tydliga: priset på polykarbonat är tillräckligt högt för att minimera mängden avfall.
Uppenbarligen kommer produkten av sektorn och radien i detta fall att vara lika med P/pi*180.
Låt oss försöka passa in bågen under ett standardark 6 meter långt. 6/3,14*180=343,9 (med avrundning). Vidare - ett enkelt urval av värden med en kalkylator i handen: till exempel för en bågsektor på 180 grader kan du ta radien lika med 343,9 / 180 \u003d 1,91 meter; med en radie på 2 meter kommer sektorn att vara lika med 343,9 / 2 \u003d 171,95 grader.
Beräkning med ackord
Hur ser beräkningen av utformningen av en polykarbonatkapell med en båge ut om vi bara har information om avståndet mellan bågens kanter och dess höjd?
I detta fall tillämpas den så kallade Huygens-formeln. För att använda det, låt oss mentalt dela ackordet som förbinder ändarna av bågen på mitten, varefter vi ritar en vinkelrät mot ackordet i mitten.
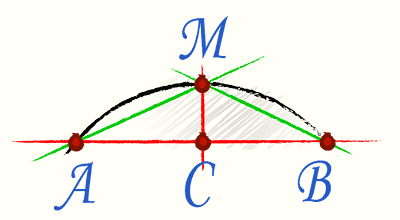
Formeln i sig har formen Р=2l+1/3*(2l-L), där l är AM-ackordet och L är AB-ackordet.
Viktigt: beräkningen ger ett ungefärligt resultat. Det maximala felet är 0,5 %; ju mindre bågens vinkelsektor är, desto mindre är felet.
Låt oss beräkna längden på bågen för fallet när AB \u003d 2 m och AM - 1,2 m.
P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 meter.
Beräkning av sektionen med känd böjlast
En ganska livssituation: en del av kapellet är ett visir av känd längd. Vi kan grovt uppskatta den högsta snöbelastningen på den. Hur väljer man ett profilrör av en sådan sektion för balkar så att det inte böjs under belastning?

Notera! Vi berör medvetet inte hur man beräknar belastningen på kapellet. Bedömning av snö- och vindbelastning är ett helt självförsörjande ämne för en separat artikel.
För att beräkna behöver vi två formler:
- M = FL, där M är böjmomentet, F är kraften som appliceras på änden av spaken i kilogram (i vårt fall, vikten av snön på visiret), och L är spakens längd (längden av balken som bär lasten från snön, från kant till spetsfästen) i centimeter.
- M/W=R, där W är motståndsmomentet och R är materialets styrka.
Och hur kommer denna hög med okända värden att hjälpa oss?
I och för sig, ingenting. Vissa referensdata saknas för beräkningen.
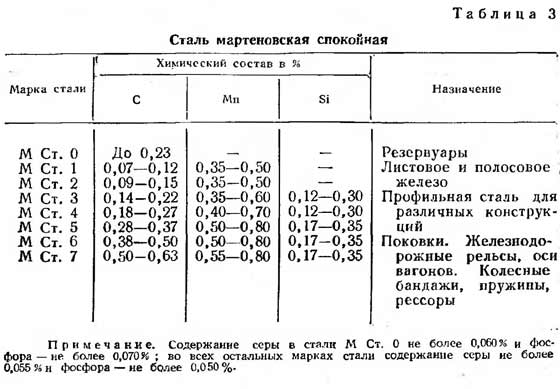
| stål grad | Styrka (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Referens: St3, St4 och St5 stål används vanligtvis för professionella rör.
Nu, baserat på de data vi har, kan vi beräkna böjmotståndsmomentet för profilröret. Låt oss göra det.
Antag att 400 kilo snö samlas på ett tvåmeterstak med tre bärande balkar av St3-stål.För att förenkla beräkningarna kommer vi överens om att hela lasten faller på visirets kant. Uppenbarligen kommer belastningen på varje balk att vara 400/3=133,3 kg; med en två-meters spak kommer böjmomentet att vara lika med 133,3 * 200 \u003d 26660 kgf * cm.
Nu beräknar vi motståndsmomentet W. Av ekvationen 26660 kgf * cm / W = 2100 kgf / cm2 (stålhållfasthet) följer att motståndsmomentet bör vara minst 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Hur kommer värdet av motståndsmomentet att leda oss till rörets dimensioner? Genom sortimentstabellerna som finns i GOST 8639-82 och GOST 8645-68 reglerar dimensionerna av fyrkantiga och formade rör. För varje storlek indikerar de motsvarande motståndsmoment och för en rektangulär sektion - längs var och en av axlarna.
Efter att ha kontrollerat tabellerna får vi reda på att minsta storleken på ett fyrkantigt rör med de nödvändiga egenskaperna är 50x50x7,0 mm; rektangulär (med vertikal orientering av den större sidan) - 70x30x5,0 mm.

Slutsats
Vi hoppas att vi inte har överarbetat läsaren med ett överflöd av torra siffror och formler. Som alltid kan ytterligare information om metoderna för att beräkna och designa polykarbonatkapell hittas i videon i den här artikeln. Lycka till!
Hjälpte artikeln dig?